Iris Classification Tour De Force

Iris Dataset - Modeling, Classification and Visualization Tour De Force¶

Everyone that has even dabbled in data science has at the very least heard of the Iris dataset. It is extremely well documented as a database used in pattern recognition and is one of the seminal and fundamental pieces of literature in the field.

The dataset looks at the petal and sepal lengths/width in cm, for 3 different types of Iris flowers (setosa, virginica, and versicolour). Each type of Iris has 50 observations associated with it.

Given that, the common question that is posed when dealing with this dataset is:

"Given a sepal length and width as well as a petal length and width for an Iris flower, can you classify it as setosa, virginica, or versicolour?"

Since flower class is not a continuous variable then this is clear a classification question that we are being asked to answer.

In this post, I'll be exploring a wide variety of classifiers and explore their hyperparameters to get a gauge of how they influence the classification accuracy. For instance, I'll make a deep learning model and checking the learning/optimization curves for it. I'll also be playing around with visualizations and statistics.

Here are some of the things I'll cover in this post:

• Exploratory Data Analysis
• Data Visualization
• Constructing, Evaluating, and Optimizing Classifier Models
• Interpreting Results of ML Classifier with ELI5
• ROC-AUC Curves
• 1D and 2D Partial Density Plots
• SHAP Values
• Principal Component Analysis
• Linear Discriminant Analysis
• Deep Learning for Multiclass Classification

With that said, let's go!

Modules Used in this Project¶

In [574]:

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from tqdm import *

#For Exploratory Data Analysis (EDA)
from pandas_profiling import ProfileReport

#For feature selection
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#For data splitting
from sklearn.model_selection import train_test_split, RepeatedStratifiedKFold, cross_val_score
from sklearn import preprocessing

# Get ML  classifiers
from sklearn.linear_model import Perceptron
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier 
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier

#Get model metrics for model evaluation
from sklearn.metrics import confusion_matrix, mean_squared_error, r2_score, accuracy_score
from sklearn.metrics import classification_report, roc_curve, auc
from sklearn.model_selection import cross_val_predict
from sklearn.decomposition import PCA
from sklearn.metrics.pairwise import cosine_similarity

#For confusion matrix display
import scikitplot as skplt

#For parameter grid search optimization
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score

#For simplified understanding of the importance model features
import eli5
from eli5.sklearn import PermutationImportance

#For generating partial dependence plots
from pdpbox import pdp, info_plots

#For calculation of shap values to further assess contributions of model features 
import shap
shap.initjs()

# import networkx library
import networkx as nx

#for venn diagrams
from matplotlib_venn import venn2

#For principal component analysis (PCA)
from sklearn.decomposition import PCA
from sklearn.metrics.pairwise import cosine_similarity

#For Linear Discrimination Analysis
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 

#For Neural Network
import tensorflow as tf
from tensorflow.keras import layers
from sklearn.preprocessing import LabelEncoder
from keras.optimizers import Adam, SGD, Adagrad

In [459]:

df = pd.read_csv("iris.data",
                 header = None, 
                 names = ['sepal_length','sepal_width','petal_length','petal_width','class'])
df

Out[459]:

	sepal_length	sepal_width	petal_length	petal_width	class
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginica
147	6.5	3.0	5.2	2.0	Iris-virginica
148	6.2	3.4	5.4	2.3	Iris-virginica
149	5.9	3.0	5.1	1.8	Iris-virginica

150 rows × 5 columns

In [16]:

df.reset_index(drop=True, inplace=True) #Drop index prior to generating report
report = ProfileReport(df)
report

Summarize dataset:   0%|          | 0/5 [00:00<?, ?it/s]

Generate report structure:   0%|          | 0/1 [00:00<?, ?it/s]

Render HTML:   0%|          | 0/1 [00:00<?, ?it/s]

Out[16]:

Lovely. No missing values and the data is uniformly distributed. If only all data was like this lol

From this report we can see that all of our numerical variables are highly correlated with one another.

We can also see from the generated histograms that the sepal length and width are normally distributed. However, the petal length and width are clearly divided into two separate distributions (is this an opportunity to apply clustering techniques?)

Let me generate a pair plot to get a birds-eye view of these interactions.

In [26]:

g = sns.pairplot(df, hue='class', diag_kind="hist", markers=["o", "s", "D"])
g.map_lower(sns.kdeplot, levels=4, color=".2")

Out[26]:

<seaborn.axisgrid.PairGrid at 0x2451aafc988>

Hmm, very nice! Here's a few things that we can readily see from this plot.

Sepal length and sepal width are highly intermixed for the classes versicolor and virginica. As such, this would make classifying the iris classes through this difficult.

Sepal length and petal length exhibit good separation between them (look at the KDE contours) and thus, could lead to accurate classification.

Petal width and petal length also exhibit good separation between them and could also lead to accurate classification between them.

Let's take a look at the violin plots to get a better idea of the probability densities of the features.

In [30]:

plt.figure(figsize=(15,10))
plt.subplot(2,2,1)
sns.violinplot(x='class', y='petal_length',data=df)
plt.subplot(2,2,2)
sns.violinplot(x='class', y='petal_width',data=df)
plt.subplot(2,2,3)
sns.violinplot(x='class', y='sepal_length',data=df)
plt.subplot(2,2,4)
sns.violinplot(x='class', y='sepal_width',data=df)

Out[30]:

<AxesSubplot:xlabel='class', ylabel='sepal_width'>

From here we can see the following:

• Sepal length for virginica spans approximately 4-9 centimeters. This is not good for maximizing separability.
• Sepal width for all 3 classes overlap a fair bit and would thus make ensuring separability difficult.
• Petal length and petal widths for all 3 classes are well separated from one another. This provides more support for choosing them as the basis of our classification models.

In [291]:

df.columns

Out[291]:

Index(['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class'], dtype='object')

Playing With Visualizations¶

Now I'm just going to play around with visualizations for a bit.

2D Density Plots¶

In [301]:

names = ['sepal_length','sepal_width','petal_length','petal_width']
f, ax = plt.subplots(4,3,figsize=(12, 14))
ax = ax.ravel()
for i in range(3):
    features = df.columns[1:4]
    sns.kdeplot(df[names[0]], df[features[i]], cmap="Reds", shade=True, bw=.15, ax = ax[i])
    
    features = list(df.columns[0:1]) +  list(df.columns[2:4])
    sns.kdeplot(df[names[1]], df[features[i]], cmap="Blues", shade=True, bw=.15, ax = ax[i+3])
    
    features = list(df.columns[0:2]) +  list(df.columns[3:4])
    sns.kdeplot(df[names[2]], df[features[i]], cmap="Purples", shade=True, bw=.15, ax = ax[i+6])
    
    features = df.columns[0:4]
    sns.kdeplot(df[names[3]], df[features[i]], cmap="Greens", shade=True, bw=.15, ax = ax[i+9])
plt.show()

Bar Plots¶

In [305]:

f, ax = plt.subplots(2,2,figsize=(9, 8))
ax = ax.ravel()
features = df.columns[:4]
i = 0
for feature in features:
    sns.despine(f)
    sns.barplot(x='class', y=feature, data=df, palette='magma', ax = ax[i])
    i += 1
plt.show()

Horizontal Bar Plots¶

In [306]:

f, ax = plt.subplots(2,2,figsize=(18, 8))
ax = ax.ravel()
features = df.columns[:4]
i = 0
for feature in features:
    sns.despine(f)
    sns.barplot(x=feature, y='class', data=df, palette='magma', ax = ax[i], orient='h')
    i += 1
plt.show()

Heatmaps¶

In [232]:

f= plt.figure(figsize=(6, 5))
sns.heatmap(df.drop(['class'], axis=1).corr())
plt.show()

Network Chart¶

Network charts are useful for seeing correlations in a similar way to a heatmap. If a quantity is closely related to another one then they'll be connected by an edge (i.e., a line). As we have seen before, the variables that make up the Iris dataset are all correlated to one another and hence the resulting network shows connections between all of them.

In [321]:

# Calculate the correlation between individuals.
corr = df.iloc[:,0:4].corr()

# Transform it in a links data frame (3 columns only):
links = corr.stack().reset_index()
links.columns = ['var1', 'var2','value']

# correlation
threshold = -1

# Keep only correlation over a threshold and remove self correlation (cor(A,A)=1)
links_filtered=links.loc[ (links['value'] >= threshold ) & (links['var1'] != links['var2']) ]
 
# Build your graph
G=nx.from_pandas_edgelist(links_filtered, 'var1', 'var2')
 
# Plot the network
nx.draw_circular(G, with_labels=True, 
                 node_color='purple', 
                 node_size=300, 
                 edge_color='black', 
                 linewidths=12, 
                 font_size=12)

Venn Diagrams¶

A Venn diagram is used to show the logical relation between sets.

In [327]:

sepal_length = df.iloc[:,0]
sepal_width  = df.iloc[:,1]
petal_length = df.iloc[:,2]
petal_width  = df.iloc[:,3]
# First way to call the 2 group Venn diagram
venn2(subsets = (len(sepal_length)-15, len(sepal_width)-15, 15),
      set_labels = ('sepal_length', 'sepal_width'))
plt.show()

In [345]:

df

Out[345]:

	sepal_length	sepal_width	petal_length	petal_width	class
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	Iris-virginica
146	6.3	2.5	5.0	1.9	Iris-virginica
147	6.5	3.0	5.2	2.0	Iris-virginica
148	6.2	3.4	5.4	2.3	Iris-virginica
149	5.9	3.0	5.1	1.8	Iris-virginica

150 rows × 5 columns

Cluster Map¶

Plot a matrix dataset as a hierarchically-clustered heatmap.

In [346]:

features = df.columns[:4]
# cluster map (dendogram and tree)
df2  = df.loc[:,features]
df1  = df['class']
x = dict(zip(df1.unique(),"rgb"))
row_colors = df1.map(x)
cg = sns.clustermap(df2,row_colors=row_colors,figsize=(12, 12),metric="correlation")
plt.setp(cg.ax_heatmap.yaxis.get_majorticklabels(),rotation = 0,size =8)
plt.show()

Building and Testing Classifier Models for Iris Dataset¶

Now let's build some models!

In [195]:

def model_assess(X_train, X_test, y_train, y_test, model, title = "Default"):
    
    model.fit(X_train, y_train)
    
    preds_test  = model.predict(X_test)
    preds_train = model.predict(X_train) 
    
    cm = confusion_matrix(y_test, preds_test)
    
    sensitivity = cm[0,0]/(cm[0,0]+cm[1,0])
    specificity = cm[1,1]/(cm[1,1]+cm[0,1])
    
    #print('Accuracy', title, ':', round(accuracy_score(y_test, preds), 5), '\n')
    score = round(accuracy_score(y_test, preds_test), 5);
    
    rf_results = pd.DataFrame([title,score,sensitivity,specificity]).transpose()
    rf_results.columns = ['Method','Training Score', 'Sensitivity', 'Specificity']

    return preds_train, preds_test, rf_results

def multi_model_assess(df, models, y_predict):
    all_model_results = [] #This will contain all model results for each dependent variable 
    all_X_test  = []
    all_X_train = []
    all_y_test_p  = []
    all_y_train_p = []
    all_y_train = []
    #First loop will define dependent/independent variables and split data into test/training sets
    n_vars = len(y_predict)
    
    for dependent in y_predict:
        model_results = [] #Array with dataframes for a given dependent variable
        #Designate independent and dependent variables
        x  = df.drop([dependent], axis = 1)
        y  = df[dependent]
        #Split data into test and training sets
        X_train, X_test, y_train, y_test = train_test_split(x, y, 
                                                            test_size = 0.2, 
                                                            )
        
        #Populate the array of observed values for the dependent variable
        all_y_train.append(y_train)
        
        pbar = tqdm(range(len(models)), desc="Variable Processed", position = 0, leave = True)#Add progress bar 
        #Process each of the desired models
        for model, model_name in models:
            if model_name == 'XGBoost':
                le = preprocessing.LabelEncoder()
                le.fit(y_train)
                y_train = le.transform(y_train)
                le.fit(y_test)
                y_test = le.transform(y_test)
                
            y_train_pred,y_test_pred, results = model_assess(X_train, X_test, y_train, y_test, model, title = model_name)
            
            model_results.append(results)
            all_X_test.append(X_test)
            all_X_train.append(X_train)
            all_y_test_p.append(y_test_pred)
            all_y_train_p.append(y_train_pred)
            pbar.update(1)       
        all_model_results.append(model_results)
        #pbar.update(1)
        #pbar.refresh()
        
    pbar.close()   
    return all_model_results, all_X_test, all_X_train, all_y_test_p, all_y_train_p, all_y_train

I anticipate all of these models to perform excellently. Therefore, I'll just run them with their default parameters. I'll initiate them below and run them.

In [202]:

lp = Perceptron()
nb = GaussianNB()
rf = RandomForestClassifier()
xg = XGBClassifier()
kn = KNeighborsClassifier()
dt = DecisionTreeClassifier()
gb = GradientBoostingClassifier()
gp = GaussianProcessClassifier()
sv = SVC()
nn = MLPClassifier()

models =  [(lp,'Perceptron'), 
           (nb,'GaussianNB'), 
           (rf,'Random Forest'), 
           (xg,'XGBoost'),
           (kn,'K Neighbors'), 
           (dt,'DecisionTree'), 
           (gb,'Gradient Boosting'), 
           (gp,'GaussianProcess'), 
           (sv,'SVC'), 
           (nn,'MLP')]

y_predict  = ['class']

all_model_results, _, _, all_y_test_p, all_y_train_p, all_y_train = multi_model_assess(df,
                                                                                       models, 
                                                                                       y_predict)

Variable Processed: 100%|██████████████████████████████████████████████████████████████| 10/10 [00:00<00:00, 21.33it/s]

Generating all these models took less than a second. Let's see how they performed.

In [203]:

score_df_results = pd.concat(all_model_results[0],
                ignore_index=True).sort_values('Training Score',axis = 0, ascending = False)
score_df_results

Out[203]:

	Method	Training Score	Sensitivity	Specificity
4	K Neighbors	1.0	1.0	1.0
7	GaussianProcess	1.0	1.0	1.0
8	SVC	1.0	1.0	1.0
2	Random Forest	0.96667	1.0	1.0
3	XGBoost	0.96667	1.0	1.0
5	DecisionTree	0.96667	1.0	1.0
6	Gradient Boosting	0.96667	1.0	1.0
9	MLP	0.96667	1.0	1.0
1	GaussianNB	0.93333	1.0	1.0
0	Perceptron	0.73333	1.0	0.928571

As expected, all models performed excellently. The Perceptron model however did perform much worse than the rest.

Brief exploration of parameter space on classification accuracy¶

Since generating these models is quite fast, I think it'd be nice to explore the effect that different parameters have on the classification accuracy. Let's check that out for a few of those models.

In [349]:

#Split data
x = df.drop(['class'], axis = 1)
y = df['class']
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)

#Define iterator parameters
max_depth_list = [1,2,3,4,5,6,7,8,9,10]
k_list = list(range(1,11))
hidden_layer_sizes_list = [25,50,75,100,125,150,175,200,250,300]

#Create dataframes to hold results
a = pd.Series(); b = pd.Series()
c = pd.Series(); d = pd.Series()
e = pd.Series(); f = pd.Series()

#Plot accuracy for each model as parameter varies
fig, ax = plt.subplots(2,3,figsize = (10, 5))
ax = ax.ravel()

#Random Forest 
for j in range(len(max_depth_list)):
    rfc=RandomForestClassifier(max_depth=max_depth_list[j]).fit(X_train,y_train)
    prediction=rfc.predict(X_test)
    a = a.append(pd.Series(accuracy_score(prediction,y_test)))
ax[0].plot(max_depth_list,a, marker = 'o')
ax[0].set_title('Random Forest')

#K-Neighbors
for j in list(range(1,11)):
    knn=KNeighborsClassifier(n_neighbors=j).fit(X_train,y_train)
    prediction=knn.predict(X_test)
    b = b.append(pd.Series(accuracy_score(prediction,y_test)))
ax[1].plot(k_list,b, marker = 'o')
ax[1].set_title('K-Neighbors')

#Decision Tree
for j in range(len(max_depth_list)):
    dtc=DecisionTreeClassifier(max_depth=max_depth_list[j]).fit(X_train,y_train)
    prediction=dtc.predict(X_test)
    c = c.append(pd.Series(accuracy_score(prediction,y_test)))
ax[2].plot(max_depth_list,c, marker = 'o')
ax[2].set_title('Decision Tree')

#Gradient Boosting
for j in range(len(max_depth_list)):
    gbc=GradientBoostingClassifier(max_depth=max_depth_list[j]).fit(X_train,y_train)
    prediction=gbc.predict(X_test)
    d= d.append(pd.Series(accuracy_score(prediction,y_test)))
ax[3].plot(max_depth_list,d, marker = 'o')
ax[3].set_title('Gradient Boosting')

#MLP Classifier
for j in range(len(max_depth_list)):
    mlp=MLPClassifier(hidden_layer_sizes=hidden_layer_sizes_list[j]).fit(X_train,y_train)
    prediction=mlp.predict(X_test)
    e = e.append(pd.Series(accuracy_score(prediction,y_test)))
ax[4].plot(max_depth_list,e, marker = 'o')
ax[4].set_title('MLP')

#XGBoost Classifier
le = preprocessing.LabelEncoder()
le.fit(y_train)
y_train = le.transform(y_train)
le.fit(y_test)
y_test = le.transform(y_test)
for j in range(len(max_depth_list)):
    xgb=XGBClassifier(max_depth=max_depth_list[j]).fit(X_train,y_train)
    prediction=xgb.predict(X_test)
    f = f.append(pd.Series(accuracy_score(prediction,y_test)))
ax[5].plot(max_depth_list,f, marker = 'o')
ax[5].set_title('XGBoost')

plt.subplots_adjust(left=0.1, bottom=0.1, right=0.9, 
                    top=0.9, wspace=0.4, hspace=0.5)
plt.show()

In [350]:

model_names = ['Random Forest','K-Neighbors',
               'Decision Tree','Gradient Boosting','MLP','XGBoost']
acc_scores_df = pd.concat([a,b,c,d,e,f],axis=1,join='outer',ignore_index=True)
acc_scores_df.columns = model_names
acc_scores_df.reset_index()
acc_scores_df

Out[350]:

	Random Forest	K-Neighbors	Decision Tree	Gradient Boosting	MLP	XGBoost
0	0.566667	0.966667	0.566667	0.966667	0.9	0.933333
0	0.933333	0.966667	0.866667	0.933333	1.0	0.933333
0	0.966667	1.000000	0.966667	0.966667	1.0	0.933333
0	0.933333	0.933333	0.966667	0.966667	1.0	0.933333
0	0.966667	0.966667	0.966667	0.966667	1.0	0.933333
0	0.966667	0.933333	0.966667	0.966667	1.0	0.933333
0	0.966667	0.933333	0.966667	0.966667	1.0	0.933333
0	0.966667	0.900000	0.966667	0.966667	1.0	0.933333
0	0.966667	0.966667	0.966667	0.966667	1.0	0.933333
0	0.966667	0.933333	0.966667	0.966667	1.0	0.933333

ROC-AUC Curves¶

An ROC curve (receiver operating characteristic curve) is a graph showing the performance of a classification model at all classification thresholds

AUC provides an aggregate measure of performance across all possible classification thresholds. AUC ranges in value from 0 to 1. A model whose predictions are 100% wrong has an AUC of 0.0; one whose predictions are 100% correct has an AUC of 1.0.

In [469]:

from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import label_binarize
from sklearn.svm import LinearSVC
from sklearn import datasets

#Split the data into X and y
iris = datasets.load_iris()
X, y = iris.data, iris.target

y = label_binarize(y, classes=[0,1,2])
n_classes = 3

# shuffle and split training and test sets
X_train, X_test, y_train, y_test =\
    train_test_split(X, y, test_size=0.33, random_state=0)

# classifier
clf = OneVsRestClassifier(LinearSVC(random_state=0))
y_score = clf.fit(X_train, y_train).decision_function(X_test)

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Plot of a ROC curve for a specific class
fig, axs = plt.subplots(1,3, figsize = (14,4))
ax = axs.ravel()
for i in range(n_classes):
    ax[i].plot(fpr[i], tpr[i], label='ROC curve (area = %0.2f)' % roc_auc[i])
    ax[i].plot([0, 1], [0, 1], 'k--')
    ax[i].set_xlim([0.0, 1.0])
    ax[i].set_ylim([0.0, 1.05])
    ax[i].set_xlabel('False Positive Rate')
    ax[i].set_ylabel('True Positive Rate')
    ax[i].set_title('ROC')
    ax[i].legend(loc="lower right")
plt.show()

Using ELI5 to understand classification process¶

In [495]:

y = df['class']
x = df.drop(['class'], axis = 1)

X_train, X_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 42)

gbc = GradientBoostingClassifier()
gbc.fit(X_train, y_train)

eli5.show_weights(gbc, feature_names = X_test.columns.tolist())

Out[495]:

Weight	Feature
0.5297 ± 0.6596	petal_width
0.4463 ± 0.6619	petal_length
0.0190 ± 0.3222	sepal_width
0.0050 ± 0.2898	sepal_length

From here we can see that petal_width and petal_length are the most heavily weighted (i.e, most important) features that the model is using to decide how to classify things.

Partial Dependence Plots - Feature Effects On Model Prediction¶

In [477]:

base_features = df.columns.values.tolist()
base_features.remove('class')

feat_name = 'petal_length'
pdp_dist = pdp.pdp_isolate(model=gbc, dataset=X_test, model_features=base_features, feature=feat_name)
pdp.pdp_plot(pdp_dist, feat_name, ncols=3)
plt.show()

In [478]:

base_features = df.columns.values.tolist()
base_features.remove('class')

feat_name = 'petal_width'
pdp_dist = pdp.pdp_isolate(model=gbc, dataset=X_test, model_features=base_features, feature=feat_name)
pdp.pdp_plot(pdp_dist, feat_name, ncols=3)
plt.show()

In [479]:

base_features = df.columns.values.tolist()
base_features.remove('class')

feat_name = 'sepal_length'
pdp_dist = pdp.pdp_isolate(model=gbc, dataset=X_test, model_features=base_features, feature=feat_name)
pdp.pdp_plot(pdp_dist, feat_name, ncols=3)
plt.show()

In [480]:

base_features = df.columns.values.tolist()
base_features.remove('class')

feat_name = 'sepal_width'
pdp_dist = pdp.pdp_isolate(model=gbc, dataset=X_test, model_features=base_features, feature=feat_name)
pdp.pdp_plot(pdp_dist, feat_name, ncols=3)
plt.show()

2D Partial Dependence Plots¶

In [490]:

#Get interaction between st_depression and st_upslope
inter1  =  pdp.pdp_interact(model=gbc, dataset=X_test, model_features=base_features,
                            features=['petal_length', 'petal_width'])
pdp.pdp_interact_plot(pdp_interact_out=inter1, feature_names=['petal_length', 'petal_width'],
                      plot_type='contour',figsize=(20,7),
                      plot_params = {'contour_color':  'black',
                                     'cmap': 'coolwarm',},ncols = 3)
plt.show()

In [491]:

#Get interaction between st_depression and st_upslope
inter1  =  pdp.pdp_interact(model=gbc, dataset=X_test, model_features=base_features,
                            features=['petal_length', 'sepal_length'])
pdp.pdp_interact_plot(pdp_interact_out=inter1, feature_names=['petal_length', 'petal_width'],
                      plot_type='contour',figsize=(20,7),
                      plot_params = {'contour_color':  'black',
                                     'cmap': 'coolwarm',},ncols = 3)
plt.show()

In [492]:

#Get interaction between st_depression and st_upslope
inter1  =  pdp.pdp_interact(model=gbc, dataset=X_test, model_features=base_features,
                            features=['petal_length', 'sepal_width'])
pdp.pdp_interact_plot(pdp_interact_out=inter1, feature_names=['petal_length', 'petal_width'],
                      plot_type='contour',figsize=(20,7),
                      plot_params = {'contour_color':  'black',
                                     'cmap': 'coolwarm',},ncols = 3)
plt.show()

SHAP Values for Assesment of Contributions of Model Features¶

In [523]:

rforest = RandomForestClassifier(n_estimators=100,
                                 max_depth=None,
                                 min_samples_split=2,
                                 random_state=0)
rforest.fit(X_train, y_train)

# explain all the predictions in the test set
explainer = shap.KernelExplainer(rforest.predict_proba, X_train)
shap_values = explainer.shap_values(X_test)

shap.summary_plot(shap_values, X_test, plot_type="bar")

Using 105 background data samples could cause slower run times. Consider using shap.sample(data, K) or shap.kmeans(data, K) to summarize the background as K samples.

  0%|          | 0/45 [00:00<?, ?it/s]

In [540]:

fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(22,15))

axes = axes.ravel()
shap.dependence_plot('petal_length', shap_values[0],
                     X_test, interaction_index="petal_width",ax=axes[0],
                    show=False)

shap.dependence_plot('petal_length',shap_values[0],
                     X_test, interaction_index="sepal_length",ax=axes[1],
                     show=False)

shap.dependence_plot('petal_length', shap_values[0],
                     X_test, interaction_index="sepal_width",ax=axes[2],
                     show=False)

#
shap.dependence_plot('petal_width', shap_values[0],
                     X_test, interaction_index="petal_length",ax=axes[3],
                    show=False)

shap.dependence_plot('petal_width',shap_values[0],
                     X_test, interaction_index="sepal_length",ax=axes[4],
                     show=False)

shap.dependence_plot('petal_width', shap_values[0],
                     X_test, interaction_index="sepal_width",ax=axes[5],
                     show=False)
#
shap.dependence_plot('sepal_length', shap_values[0],
                     X_test, interaction_index="petal_length",ax=axes[6],
                    show=False)

shap.dependence_plot('sepal_length',shap_values[0],
                     X_test, interaction_index="petal_width",ax=axes[7],
                     show=False)

shap.dependence_plot('sepal_length', shap_values[0],
                     X_test, interaction_index="sepal_width",ax=axes[8],
                     show=False)

In [517]:

shap.force_plot(explainer.expected_value[0], shap_values[0], X_test)

Out[517]:

Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

Linear Discriminant Analysis (LDA)¶

In [573]:

# fitting the model
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values

model = LinearDiscriminantAnalysis()
model.fit(X, y)

# evaluating the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
print(np.mean(scores))

X = iris.data
y = iris.target
model = LinearDiscriminantAnalysis()
data_plot = model.fit(X, y).transform(X)
target_names = iris.target_names


plt.figure()
colors = ['red', 'green', 'blue']
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(data_plot[y == i, 0], data_plot[y == i, 1], alpha=.8, color=color,
                label=target_name)

plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.show()

0.9800000000000001

Principal Component Analysis¶

In [580]:

x = df.drop(['class'], axis = 1)
y = df['class']

#### NORMALIZE X ####
cols = x.columns
min_max_scaler = preprocessing.MinMaxScaler()
np_scaled = min_max_scaler.fit_transform(x)
x = pd.DataFrame(np_scaled, columns = cols)


#### PCA 2 COMPONENTS ####
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents, columns = ['principal component 1', 'principal component 2'])

# concatenate with target label
finalDf = pd.concat([principalDf, y], axis = 1)

pca.explained_variance_ratio_

plt.figure(figsize = (16, 9))
sns.scatterplot(x = "principal component 1", 
                y = "principal component 2", 
                data = finalDf, 
                hue = "class", alpha = 0.7,
               s = 100);

plt.title('PCA', fontsize = 25)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 10);
plt.xlabel("Principal Component 1", fontsize = 15)
plt.ylabel("Principal Component 2", fontsize = 15)

Out[580]:

Text(0, 0.5, 'Principal Component 2')

Iris Classification with Tensorflow (Because why not?)¶

Yeah, this is overkill, but it's kinda funny so I'm going to do it lol I'm going to build a neural network to classify the Iris dataset. The Neural Network is going to have the following structure:

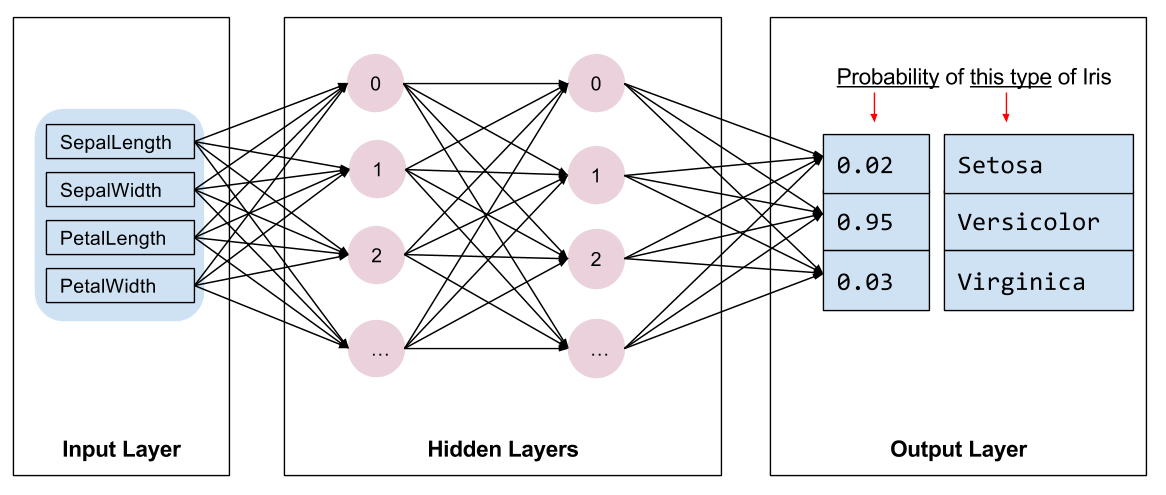
The input layer is composed of 4 nodes because we are using 4 features as part of the model. The output layer has 3 nodes because there are 3 classes of Iris flowers. The number of hidden layers as well as their properties is what will make a neural network unique.

I'll also make sure I'm using my GPU because might as well go all out at this point right?

In [386]:

print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))

Num GPUs Available:  1

Cool. GPU is ready to rock. Let's create the X and Y sets. X are going to be the each of the 4 numerical attributes we have for each flower. Y will be the Iris classes.

In [368]:

#Split the data into X and y
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
print(X.shape)
print(y.shape)

(150, 4)
(150,)

Since the 'class' is a categorical variable, we need to one hot encode it so that it can be parsed by the keras/tensorflow API.

In [370]:

encoder =  LabelEncoder()
y1 = encoder.fit_transform(y)

Convert target into one hot encoding

In [371]:

Y = pd.get_dummies(y1).values

Now I'll convert X and Y into train and test data using an 80/20 split

In [560]:

X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

Build the model

In [561]:

model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, activation='relu', input_shape=(4,)),#Input layer has 4 nodes
    tf.keras.layers.Dense(10, activation='relu'),
    tf.keras.layers.Dense(3, activation='softmax') #Output layer has 3 nodes
  ])

Compile the model

In [562]:

opt = Adagrad(lr = 0.1)
model.compile(optimizer=opt,
              loss='categorical_crossentropy',
              metrics=['accuracy'])

Train and evaluate the model

In [563]:

history = model.fit(X_train,
                    y_train, 
                    batch_size=64, 
                    epochs=200, 
                    verbose = 0)

loss, accuracy = model.evaluate(X_test, y_test, verbose=0)
print('Test loss:', loss)
print('Test accuracy:', accuracy)

Test loss: 0.030577950179576874
Test accuracy: 1.0

What do you know... 100% classification accuracy lol

Let's see the accuracy and loss over time to see how the model is learning

In [564]:

fig, axes = plt.subplots(2, sharex=True, figsize=(12, 8))
fig.suptitle('Training Metrics')

axes[0].set_ylabel("Loss", fontsize=14)
axes[0].plot(history.history['loss'])

axes[1].set_ylabel("Accuracy", fontsize=14)
axes[1].set_xlabel("Epoch", fontsize=14)
axes[1].plot(history.history['accuracy']);

Our loss function is being minimized and the model accuracy is being maximized over time. In other words, the model is learning well.

Let's test the model

In [390]:

y_pred = model.predict(X_test)

1/1 [==============================] - 0s 15ms/step

And let's a take a look at the predictions.

In [395]:

actual = np.argmax(y_test,axis=1)
predicted = np.argmax(y_pred,axis=1)
print(f"Actual   : {actual}")
print(f"Predicted: {predicted}")

Actual   : [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0]
Predicted: [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0]

The model matches the actual observations perfectly.

Conclusions¶

This was just a neat little showcase of classification techniques and ways to visualize, optimize, and interpret the resulting models. As you can see, there's a treasure trove of information that can be extracted for even a small and deceptively simple dataset as this one.

Hope you had fun!